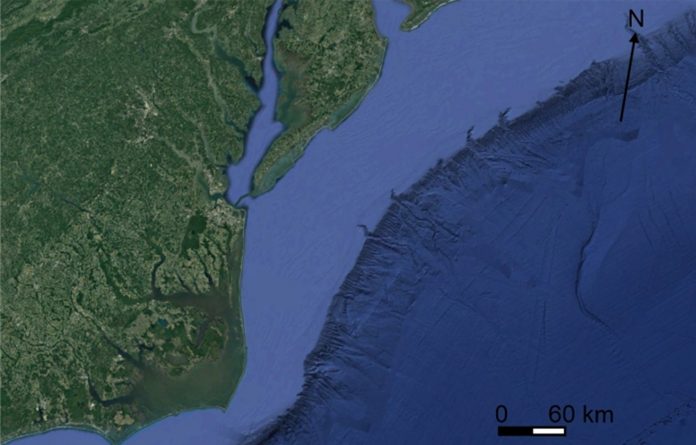
Figur 1: Kontinentalmarginen utenfor USAs kyst med dens bratte skråning ned til dyphavssletten (fra Google Earth)
Vi kunne nesten ikke vært mer ulike, jeg og Alessandro. Han høy, mørkhåret, amerikansk briljant ekstrovert professor i geofysikk, jeg blond, nystartet, forvirret svensk PhD-student i geologi. Men hvor lå egentlig den største forskjellen? I at han var mann? I hans ansiennitet?
Nei. Den største forskjellen lå i ordet etter geo; han var fysiker, matematiker. Hans formler og integraler, Poissons forhold og divergerende vektorer spredde seg over tavlen, og over side etter side i min notatbok og mot slutten av timen sa han glatt «og nå ser dere helt sikkert hva dette fører til?». Kort svar, nei, jeg hadde ingen anelse.
I geologi observerer vi, tar på, føler oss fram. 4,6 milliarder år pusles sammen gjennom iherdig, tålmodig, systematisk observasjon og analyse. Steinene har en historie, og vi vil lytte, vi vil lese. Men for oss er det også så åpenbart at hver stein har sin egen historie, og stemmene blandes, skriker forskjellige ting, sider i boken mangler, har blitt revet ut og spredt med vinden. Puslespillet er ufullstendig, vanskelig å tolke, og komplekst.
Matematikken står i sterk kontrast. Tall og formler leder fram til ett svar. Likhetstegnet gjenspeiler balanse på begge sider.
Ofte møtes de. Verden, naturen, steinene, og matematikken, fysikken, formlene. Det er i menneskenes natur å ville forstå og forklare. Den typen forståelse driver vår kunnskap, driver menneskeligheten fremover. Leder til å kunne systematisere, automatisere, og forutsi. Vi har reist til månen. Vi vet når Halley’s komet kommer tilbake. Vi kan forutsi været, tsunamier, klimaforandringer. Listen er uendelig. Men kan vi forklare uten å forenkle?
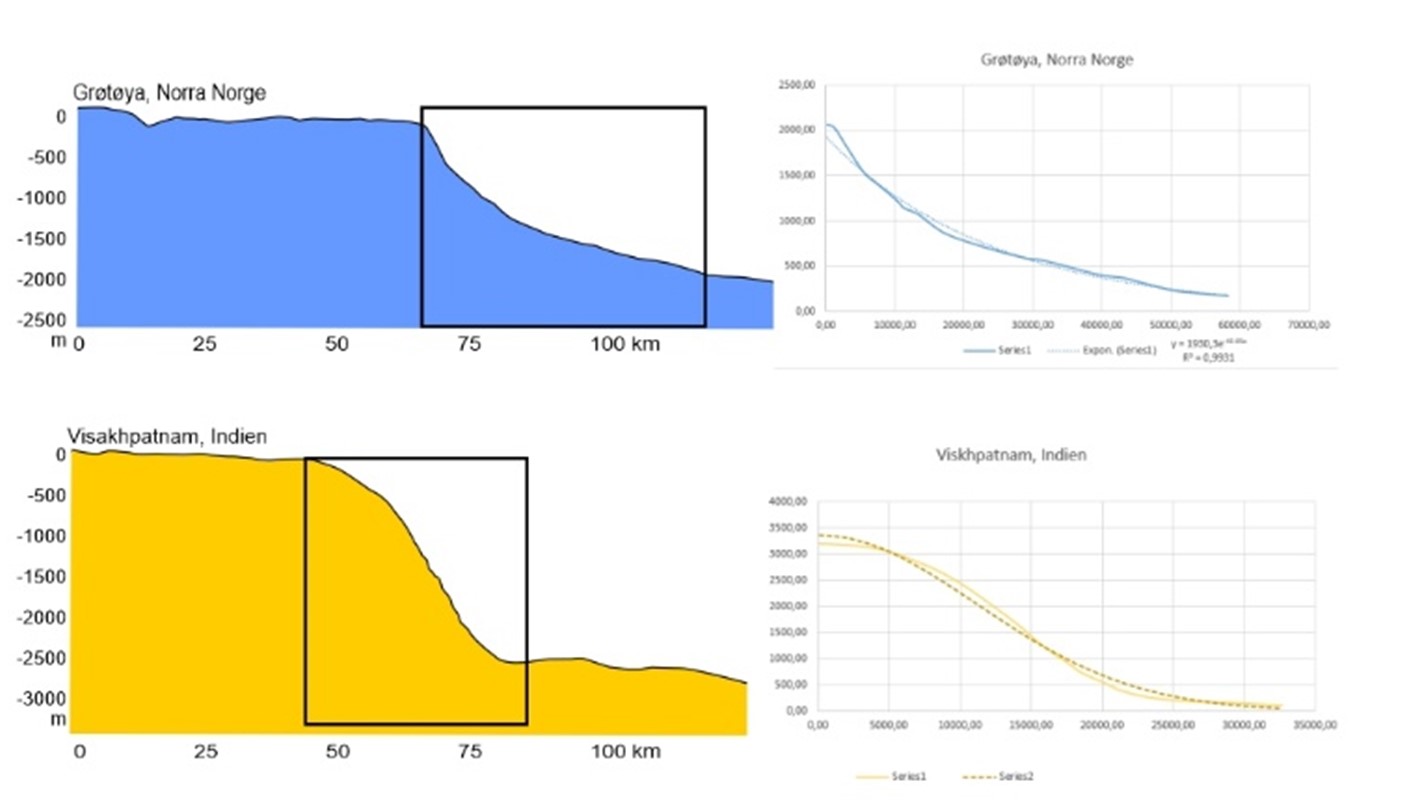
Utenfor våre kontinenter ender kontinentalmarginen i de dypeste havene (Fig. 1). Her finner vi gjentakende lignende skråninger. Det som er fascinerende er at de ser akkurat ut som matematiske funksjoner. Akkurat som dem som dukket opp på Texas Instruments kalkulatoren på videregående. Og vi kan tilpasse matematiske likninger til dem. Tilnærmet perfekt (Fig. 2). Skråninger der kurvaturen igjen og igjen gjenspeiles av et fåtall funksjoner: eksponentielle, lineære, kvadratiske eller Gaussiske (normal distribusjon).
Men hva betyr det egentlig? Ingen skråninger er nøyaktig lik den neste – sokkelen har ulik bredde, skråninger har ulike lengde, dypet varierer, iblant er det bratt som en klippevegg og iblant lavere enn de fleste grønne bakker på fjellet. Samtidig kan vi matematisk kategorisere dem. Og i dette må det finnes informasjon.
Sediment dannes kontinuerlig, berg forvitres, og vind og vann og gravitasjon transporterer det. Delene brytes ned, mineraler løses opp og gjennom et delvis haltende langstrakt transportbånd flyttes sediment ned i det dypeste havet. Likeså flyttes også forurensninger, mikroplast, og miljøgifter ned. Men hvor har vi erosjon, kollaps og skred? Hvor får vi avsetning, hvor raskt og hvilken type? Hvor samles giftige stoffer, og hvordan påvirkes flora og fauna i de dypeste mest uutforskede steder på jordkloden?
Om vi kan kategorisere kontinentalgrensene kan vi kanskje, bare ved hjelp av en enkel topografisk profil, forutsi hvilke prosesser som pågår med tanke på transport, erosjon og avsetning av sediment. Og siden disse prosessene er avhengige av for eksempel regn, stormer, havnivå, bølger, vanntemperatur, havstrømmer, salinitet etc. som i sin tur endres med klimaendringene, blir det desto viktigere å øke forståelsen.
Sokkelen rundt kontinentene er av enorm økonomisk betydning; fiske, turisme, ressurser som olje, gass og mineraler, samtidig som de er områder med store forurensningsproblemer.
Timen nærmer seg slutten og Alessandro presenterer en matematisk modell av dynamisk topografi, altså høyder og forsenkninger på jordskorpen drevet av konveksjon i mantelen. Han forteller at modellen vitner om enorme områder som burde være høyere eller lavere enn de er.
Geofysikkgruppen starter en engasjert diskusjon om hvilke krefter som forhindrer dette. Jeg, den eneste geologen i rommet, tør nesten ikke å spørre; kan det ikke være sånn at det bara er modellen som er feil? Eller i dette tilfellet, kommer ikke alle individuelle sedimentkorn, som har fulgt helt unike langstrakte transportreiser, og blir utsatt for helt unike hydrodynamiske forhold å danne en helt unik skråning? Kan naturen virkelig gjenspeiles av en matematisk formel? Er naturen ikke for mangefasettert til å forenkles til en s-formet kurve på et papir.
Jeg plotter inn en ny profil og funderer videre. For svaret har jeg ikke funnet ennå.
Stort tack till Karianne Staalesen Lilleøren för norskifisering av en svorsk text.

Ingrid Anell er førsteamanuensis i sedimentologi ved Institutt for geofag ved Universitetet i Oslo.
Dette er hennes bidrag til formidlingskonkurransen 2023.